人材採用において、候補者の優劣が付け難い場合、どの候補者を採用すべきか悩むことがあります。
選考が進んだ、最終面接のタイミングでは、後戻りができず、採用に対するプレッシャーも高いため、失敗することができません。
そのような場合は、データを活用することで、簡単にどの候補者を採用するべきか明らかにすることができます。
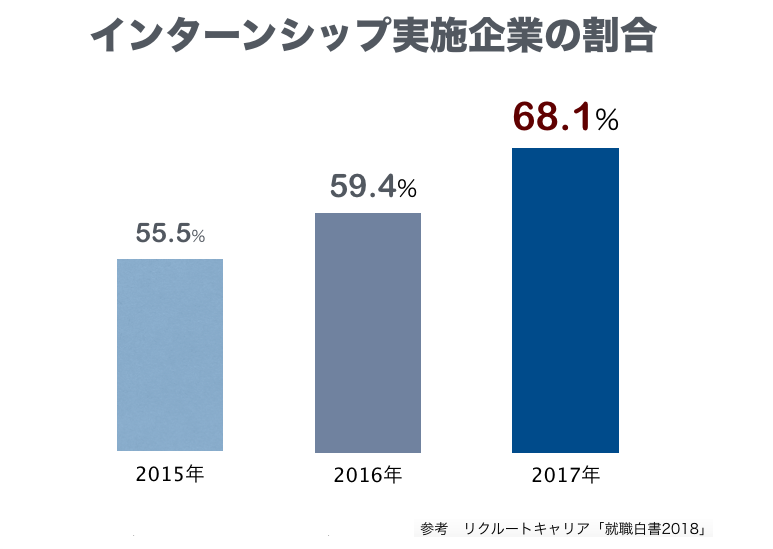
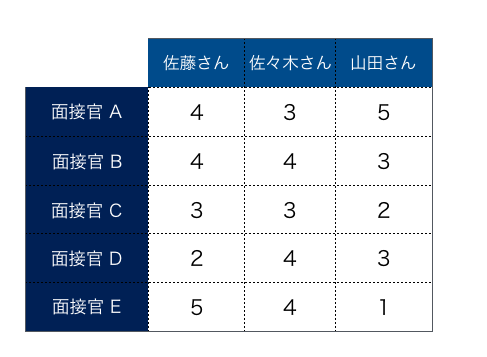
例えば、佐藤さん、佐々木さん、山田さんの候補者3名が最終選考まで残ったとします。各候補者に対する最終面接の評価得点は下記のような表になりました。
データを分析する前に、平均と標準偏差に関して説明します。
平均と標準偏差を理解する
平均と中央値
平均値とは、得点の合計をサンプル数で割ったものです。平均値は誰でもわかりやすいものですが、外れ値に引っ張られやすいというデメリットがあります。
その場合は、中央値を使います。中央値とは、データを大きい順番に並べると、真ん中に来る値のことです。平均値と比べると、外れ値の値に左右されないため、結果が安定するメリットがあります。
分散と標準偏差
分散とは、データの散らばり具合を示したものです。分散が大きいほど、データに個性があり、分散が小さいほど、データの個性が無いとも言えます。
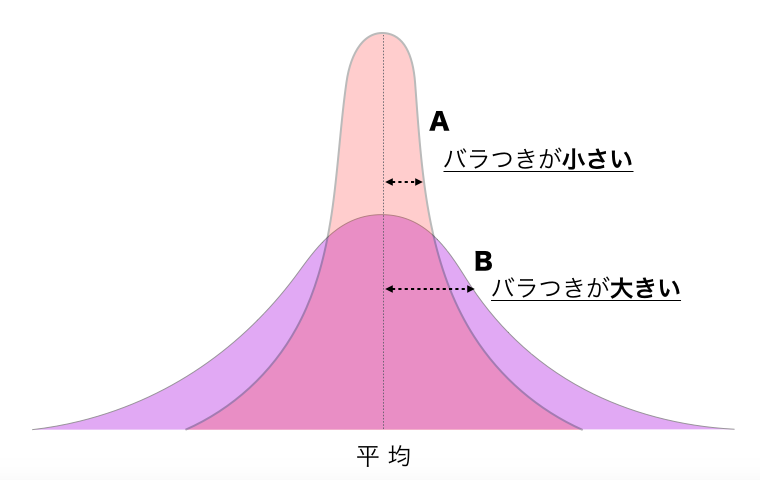
上記の図から分布Aは平均からのバラつきが少なく分散が小さいと言えます。一方、分布Bは平均からのバラつきが大きいため、分散が大きいとも言えます。
標準偏差とはこの分散を平方根(√)で計算したものです。標準偏差にすることで、単位がデータと同じにすることができます。
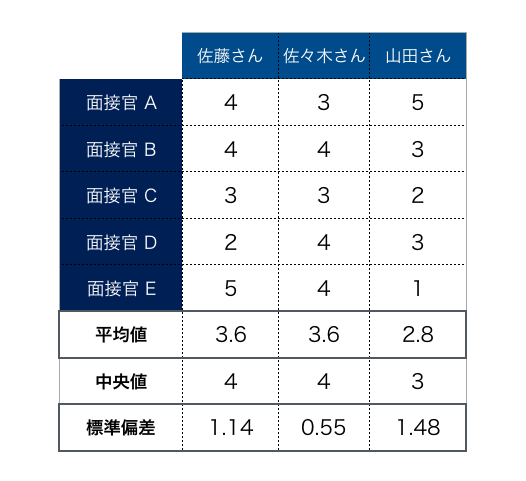
先ほどの、面接官の評価得点から、各候補者の平均、標準偏差を求めると、下記の表になります。
散布図から採用すべき候補者を見極める
まず山田さんは他の二人の候補者と比べて、得点の平均値が低いので、採用候補から外します。
問題は、佐藤さんと、佐々木さんのどちらを採用するべきか考えなければなりません。
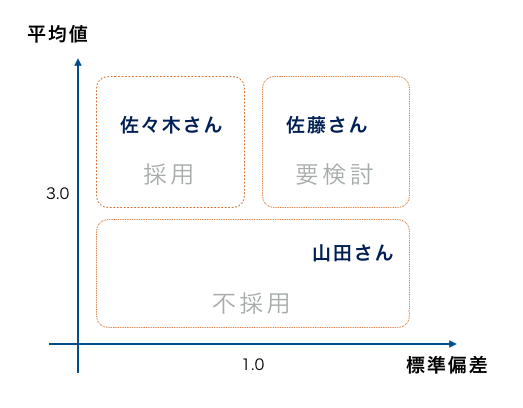
そこで、平均値と標準偏差の値を活用してx軸を標準偏差、y軸を平均値として下記のよな散布図を描きます。
佐藤さんの平均値は3.6と高く、標準偏差が大きくなっています。標準偏差が大きいということは、面接官の評価にバラつきがあるということです。
一方、佐々木さんは平均値は3.6と佐藤さんと同じですが、標準偏差が佐藤さんよりも低く、面接官の評価のバラつきが小さいことがわかります。つまり安定して良い評価を得られていることがわかります
分布図で、佐々木さんは、採用の範囲に位置しており、三人の候補者の中では佐々木さんを採用するべきとの結果になりました。
まとめ
このように、平均値と標準偏差の値を活用するだけで、客観的にどの候補者を採用するべきか明らかにすることが出来ます。
社内での面接官の意見が割れた場合に、特に有効な手段です。是非、お試しください。